【分析】可以假設(shè)圓形跑道的長為120米，那么甲的速度為120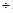
12=10(米/分)，乙的速度為120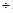15=8(米/分)，如果他們分別從圓形跑道直徑的兩端同時出發(fā)，他們在圓形跑道上的距離為60米，甲追上乙需要的時間為60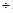（10-8）=30(分鐘)．
另解：因為乙跑一圈要15分鐘，所以把15分鐘看作一個單位進(jìn)行考慮，在15分鐘內(nèi)，乙跑了一圈，甲跑了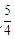
圈，甲比乙多跑了
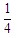圈，而開始時甲、乙兩人相距半圈，所以需要2個15分鐘，也就是30分鐘后甲可以追上乙．
編輯推薦：
-------------------------------------------------------------------------------------
《小學(xué)奧數(shù)系統(tǒng)總復(fù)習(xí)》 圖書簡介
 |
《小學(xué)奧數(shù)系統(tǒng)總復(fù)習(xí)》分 上下兩冊，涵蓋了奧數(shù)中8大專題，共設(shè)21講。每講設(shè)置4大模塊，即闖關(guān)目標(biāo)、賽前熱身、實戰(zhàn)演練和逐級闖關(guān)，構(gòu)建了完整的奧數(shù)知識體系，全面覆蓋小學(xué)奧 數(shù)知識。此外，本書對部分經(jīng)典例題錄制了視頻，免費贈送給各位學(xué)員。本書附有2010年和2011年的北京集訓(xùn)隊選拔試題，為本書增加了新的亮點。 為了讓大家更好的獲得知識、理解知識，本書設(shè)有論壇交流環(huán)節(jié)，讀者可以登錄E度論壇點擊進(jìn)入圖書答疑帖，即可實現(xiàn)在線提問、交流心得，名師天天坐鎮(zhèn)論壇，等你來交流！ |
