柯尼斯堡城是條頓騎士在1308年建立的，作為日爾曼勢力最東端的前哨達四百余年之久。第二次世界大戰后，它被更名為加里寧格勒，成了蘇聯最大的海軍基地。今天，柯尼斯堡位于立陶宛與波蘭之間（加里寧格勒現屬俄羅斯。——譯者注）。柯尼斯堡的七座橋今天看來怎么樣了？人們仍然在企圖找出不可能的路線嗎？首先，讓我們把柯尼斯堡橋問題扼要重述如下——

若干世紀以來，柯尼斯堡橋問題提供了豐富的樂趣和數學興味。問題遠溯至18世紀初。背景是位于普雷蓋爾河岸的柯尼斯堡城。河中的兩個島是城的部分，由七座橋與城連接。柯尼斯堡的居民中有一個歡樂的傳統：星期天沿著城市的河岸和島嶼散步，同時試圖找到一條路線，可以經過所有七座橋，但不重復經過任一座橋。雖然當時大多數人都把這當做有趣的娛樂，但是一位數學家發現這娛樂可以導向一個另外的契機，他抓住了這個契機并加以發展。瑞士數學家倫哈德·歐拉（1707～1783）在圣彼得堡為俄國凱瑟琳大帝服務時就知道了柯尼斯堡橋問題。

1735年，歐拉向俄國科學院提交了一篇論文，它不是簡單地解答了橋問題，而是具有更加深遠的意義，對數學產生了更加巨大的影響。他提出的新思想開辟了拓撲學的領域。拓撲學與研究大小、形狀和剛體的歐幾里得幾何不同，它是研究物體即使在大小和形狀改變時依然保持不變的那些特性的幾何學。例如，如果三角形變形為正方形或圓，拓撲學研究這對象的哪些特性保持不變。歐拉把柯尼斯堡橋問題的物理背景變換并簡化為一種數學設計（稱做圖或網絡），這設計包含這個問題，并使它簡化。對于城市與橋相通的每一部分，他用一個頂點來代表，每一座橋則用一個弧來表示。他的結論是：經過所有七座橋而不復返的問題相當于用鉛筆不離紙面地描繪整個網絡。歐拉把每個頂點定為奇頂點或偶頂點。他指出，偶頂點是路程經過這頂點即進入這頂點又離開這頂點或整個路程從這點開始又到這點結束而造成的。另一方面，奇頂點則是以這頂點成為路程的起點或終點而造成的。因此，任何可一筆畫成（沒有復返）的圖最多只能有2個奇頂點——要末沒有奇頂點，頂點都是偶頂點；要末有2個奇頂點，如果一個是起點，一個是終點。此外，他還斷定，如果這圖有偶數個奇頂點，譬如說10個，那末在描繪整個圖時，筆離開紙面的次數一定是奇頂點個數的一半，即5次。歐拉在他的論述中指出，柯尼斯堡橋問題似乎具有幾何性質，但是看來歐幾里得幾何并不適用，因為橋問題不涉及“大小”，也不能用“量化計算”來解決。相反地，這問題屬于“位置幾何”，這是戈特弗里德·威廉·馮·萊布尼茲描述拓撲學時首先用的名稱。由此可知，歐拉對柯尼斯堡橋問題的解答成了拓撲學領域的催化劑和導引。

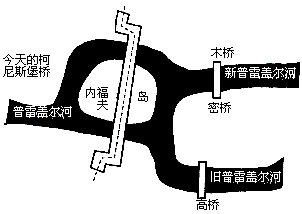
如圖所示，七座橋各有專名，大概與橋的那邊是什么有關。今天只剩下了原有七座橋中的三座——蜜橋、高橋和木橋。一條新的跨河大橋已經建成，它與兩岸的連接如圖所示，它完全跨過了內福夫島。導游們時常講述柯尼斯堡橋問題的故事。有些導游甚至聲稱它仍未解決。如果畫出新柯尼斯堡橋的網絡，這新問題是沒有吸引力的。如果新橋接觸到島的地面，網絡將比較有趣些。不幸的是，七座柯尼斯堡橋成了歷史，但是這問題留下的遺產不像這些橋那樣容易破壞。歐拉的出色的解答仍然是拓撲學發展史上的一個重要部分。

志謝：特別感謝阿爾特·庫利提供最新資料和照片，并感謝羅德·克里坦登引起我對這些資料的注意。