分析：根據(jù)題意，可設(shè)剪去的小正方形的邊長是x，可利用體積公式表示出剪去后的紙盒的體積，因?yàn)榧埡械倪呴L一定，即2x+（12-x）+（12-x）=24是一個(gè)定值，那么當(dāng)2x等于12-x時(shí)，紙盒的體積2×2x（12-x）（12-x）最大，所以計(jì)算出2x等于12-x中的未知數(shù)即可知道剪去的小正方形的邊長，列式解答即可．

　　解：如圖

　　設(shè)剪去的小正方形邊長為x厘米，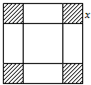                           

　　則紙盒容積為：V=x（24-2x）（24-2x），

　　=2×2x（12-x）（12-x），

　　因2x+（12-x）+（12-x）=24，

　　故當(dāng)2x=12-x時(shí)，其乘積最大，

　　2x=12-x，

　　3x=12，

　　x=4，

　　即x=4時(shí)，其乘積最大即紙盒容積也最大．

　　答：剪去的小正方形的邊長應(yīng)為4厘米．

　　點(diǎn)評：解答此題的關(guān)鍵是依據(jù)正方體的體積公式表示出這個(gè)紙盒的體積，要使體積最大算式中的2x、12-x、12-x應(yīng)該相等，所以算式中的2x等于12-x，紙盒的體積最大，解答即可．