決戰2013年小升初數學競賽解題密匙:整除問題(3)
來源:奧數網整理 2012-10-15 17:24:51

例 7 有 8 個不同約數的自然數中,最小的一個是多少?
解:設有 8 個不同約數的自然數為 N,根據例 8 后的說明來分析 N 的取 值可能性。
因為 8=7+1=(1+1)·(3+1)=(3+1)·(1+1)=(1+l)·(1+1)·(1+l),所以 N 只能為下面四種形式:
(1)N=a7 (3)N=a3×b
(2)N=a×b3 (4)N=a×b×C
(a、b、c 為不同的質數)
要使 N 最小,可以用 a=2,b=3,C=5 去代入上面四個等式,分別得到 N 為 128、54、24、30。所以有 8 個不同約數的自然數中最小的一個是 24。
答:最小的一個是 24。
例 8 (中國古代問題) 今有物不知其數,三三數之剩二,五五數之剩三,七七數之剩二,問物幾何?
這一問題可譯為:一個數除以 3 余 2,除以 5 余 3,除以 7 余 2,求適合這些條件的最小數。
解法 1:用枚舉法。
(1)除以 3 余 2 的數有:5、8、11、14、17⋯⋯;
(從第二個數起,每一個數都比它的前一個數多 3)
(2)除以 5 余 3 的數有:8、13、18、23、28、⋯⋯。
(從第二個數起,每一個數都比它的前一個數多 5)
顯然 8 被 3 除余 2,且被 5 除余 3。因為 3 與 5 的最小公倍數是 15,所 以 15+8、15×2+8⋯⋯15×n+8,都同時滿足被 3 除余 2,被 5 除余 3 這兩 個條件,只須在這列數中找到被 7 除余 2 的最小數。為此只要用 n=1、2、3、4、⋯⋯依次去代入 15×n+8。當 n=1 時,15×1+8=23,23÷7=3⋯⋯2 所以 符合題意的數是 23。
解法 2:
(1)從 5 和 7 的公倍數 35、 70、 105⋯中找出除以 3 余 2 的最小數是 35。
(2)從 3 和 7 的公倍數 21、 42、63、⋯中找出除以 5 余 3 的最小數是 63。
(3)從 3 和 5 的公倍數 15、30、45、⋯中找出除以 7 余 2 的最小數是30。
所以 35+63+30=128 能符合“被 3 除余 2、被 5 除余 3、被 7 除余 2”。 又因為 3、5、7 的最小公倍數是 105,由此得符合題意的數是 128-105×1=23。
答:適合這些條件的最小數是 23。 說明:這個問題是馳名中外的中國古代問題之一。解答這類問題要用到古代數學家孫子所發明的著名定理——“孫子定理”,它的解法很早就流傳到國外,被稱為“中國剩余定理”。
例 9 一個數減去 1 能被 2 整除,減去 2 能被 5 整除,減去 3 能被 7 整 除,加上 4 能被 9 整除,這個數最小是多少?
(1990 年江西省小學生“八一杯”數學比賽題)解:
(1)“減去 1 能被 2 整除”的數,可知這個數是奇數。
(2)“減去 2 能被 5 整除”的數,可知它的個位數是 2 或 7。
(3)“減去 3 能被 7 整除”的數,可知這個數是 10、 17、24、⋯⋯ 同時符合(1)、(2)、(3)的數是 17。
因為 2、5、7 的最小公倍數是 70,所以同時符合(1)、(2)、 (3) 的數的一般式是 70×n+17。
又因為“一個數加上 4 能被 9 整除”相當于“一個數被 9 除不足 4”, 也就是“一個數被 9 除余 9-4=5”。所以用 n=1、2、3、4、5、⋯⋯代入 70×n+17,當 n=6 時,70×6+17=437 被 9 除余 5,由此得符合題意的最小數是437。
答:這個數最小是 437。
例 10 幼兒園拿出一塊長方體木料,長 72 厘米,寬 60 厘米,高 36 厘
米,請王師傅把它鋸成同樣大小的正方體木塊,木塊的體積要最大,木料又不能剩余,算一算,可以鋸成幾塊?
(廈門市小學生 1986 年“從小愛數學”預賽題) 解:由題意可得王師傅要把原長方體木料鋸成同樣大小的正方體木塊(體積要最大),木料又不能剩余,那么鋸成的正方體的棱長必須是長方體木料的長、寬、高的最大公約數。
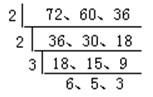
72、60、36 的最大公約數是 2×2×3=12。所以,能鋸成最大正方體的木塊數是 6×5×3=90(塊)。或(72×60×36)÷(12×12×12)90(塊)。 答:可以鋸成 90 塊。
編輯推薦:
相關文章
- 小學1-6年級作文素材大全
- 全國小學升初中語數英三科試題匯總
- 小學1-6年級數學天天練
- 小學1-6年級奧數類型例題講解整理匯總
- 小學1-6年級奧數練習題整理匯總
- 小學1-6年級奧數知識點匯總
- 小學1-6年級語數英教案匯總
- 小學語數英試題資料大全
- 小學1-6年級語數英期末試題整理匯總
- 小學1-6年級語數英期中試題整理匯總
- 小學1-6年語數英單元試題整理匯總





