決戰2013年小升初數學競賽解題密匙:算謎問題(2)
來源:奧數網整理 2012-10-15 14:10:21

例 4 下面的算式里,每個方框代表一個數字。問:這 6 個方框中的數 字的總和是多少?
(1991 年第三屆“華羅庚金杯賽”初賽試題)
分析:解決這樣的問題,我們需要認真審題,抓住式中的某些特點,尋 找突破口。
這個題目的突破口在百位上,由于十位至多向百位進 1,且百位上兩個□內數字之和加上十位向百位的進位等于 19,可以推出百位上兩個□內數字 均填 9,且十位向百位進 1;同理,由于十位上兩個□內數字之和加上個位向 十位的進位等于 19,可以推出十位上兩個□內數字均填 9,且個位向十位進1;由此推出個位上兩個□內數字之和等于 11。 解法:由于兩個加數的十位和百位數字均為 9,兩個加數的個位數字之和為 11,因此所有□內數字之和為 9×4+11=47。
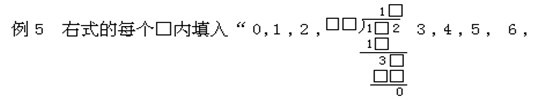
7,8,9”中的某一個數字,使得該除式成立。(上海市 1988 年小學數學競賽試題)
分析:根據除式條件,首先可知除數的十位數字是 1,第一次相除后,余數是 32,由此推出商數的個位數字只能是 2,除數的個位數字也只能是 6。
解法: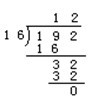
例 6 在□中填上適當的數字,使算式成立。

分析:因為除數是三位數,并且百位數為 6,它和商的首位的乘積也是 三位數,所以商的首位是 1;因為第一行的個位數是 7,所以除數的個位數也是 7; 因為第二行的個位為 1,所以商的個位為 3。因為 3×7= 21,必須向十位進 2,所以根據十位上的 6,推知除數的十位是 8。商與除數確定后,其他 數字都易于確定。
解法:
例 7 在右邊的算式中 A、B 代表不同的數字,若算式成立,求出 A、B。(1980美國長島小學數學奧林匹克競賽試題)

解法:算式中, AB×A=114 將 114 分解因式, 114=2×3×19,然后 將 114 寫成一個二位數與一個一位數的積。114=52×2=38×3=19×6,顯然 38×3 符合要求,所以 A=3,B=8。
相關文章
- 小學1-6年級作文素材大全
- 全國小學升初中語數英三科試題匯總
- 小學1-6年級數學天天練
- 小學1-6年級奧數類型例題講解整理匯總
- 小學1-6年級奧數練習題整理匯總
- 小學1-6年級奧數知識點匯總
- 小學1-6年級語數英教案匯總
- 小學語數英試題資料大全
- 小學1-6年級語數英期末試題整理匯總
- 小學1-6年級語數英期中試題整理匯總
- 小學1-6年語數英單元試題整理匯總





