奧數 > 小學試題庫 > 單元測試 > 數學單元測試 > 六年級數學單元測試上冊 > 正文
2011-11-08 16:13:00

小學數學總復習專題講解及訓練(七)
主要內容
正比例和反比例
學習目標
1、使學生結合實際情境認識成正比例和反比例的量,能根據正、反比例的意義判斷兩種相關聯的量是否成正比例或反比例。
2、使學生初步認識正比例的圖像是一條直線,能利用給出的具有正比例關系的數據在方格紙上畫出相應的直線,能根據具有正比例關系的一個量的數值看圖估計另一個量的數值。
3、使學生在認識成正比例、反比例的量的過程中,初步體會數量之間相依互變的關系,感受有效表示數量關系及其變化規律的不同數學模型,進一步提升思維水平。
4、使學生進一步體會數學與日常生活的密切聯系,增強探索數學知識和規律的意識,養成積極主動地參與學習活動的習慣,提高學好數學的信心。
考點分析
1、兩種相關聯的量,一種量變化,另一種量也隨著變化。如果這兩種量中相對應的兩個數的比的比值(也就是商)一定,這兩種量就叫做成正比例的量,它們之間的關系叫做正比例關系。
如果用字母x和y分別表示兩種相關聯的量,用k表示它們的比值,正比例關系可以用這樣的式子來表示: = K(一定)。
= K(一定)。
2、用“描點法”可以得到正比例的圖像,正比例的圖像是一條直線。對照圖像,能根據一種量的值,估計另一種量相對應的值。
3、兩種相關聯的量,一種量變化,另一種量也隨著變化。如果這兩種量中相對應的兩個數的乘積一定,這兩種量就叫做成反比例的量,它們之間的關系叫做反比例關系。
如果用字母x和y分別表示兩種相關聯的量,用k表示它們的積,反比例關系可以用這樣的式子來表示:xy = K(一定)。
4、兩個變量的比值一定,這兩個變量成正比例;兩個變量的積一定,這兩個變量成反比例;沒有上述兩種關系,這兩個變量不成比例。
典型例題
例1、(正比例的意義)一列火車行駛的時間和路程如下表。這兩種量有什么關系?

分析與解:
(1)從上表可以看出,表中有時間和路程兩種量。
(2)從左往右看,時間擴大,路程也擴大;從右往左看,時間縮小,路程也縮小。所以它們是兩種相關聯的量。
(3)路程和時間的比值始終不變, ……這個比值就是火車的行駛速度。
……這個比值就是火車的行駛速度。
通過觀察和計算,我們對路程和時間的關系有兩點發現:第一點路程和時間是兩種相關聯的量,也就是時間變化,路程也隨著變化;第二點路程和對應的時間的比的比值(也就是速度)是一定的,有這樣的關系:
具備了這兩個條件,我們就可以得到結論:行駛的路程和時間成正比例關系;行駛的路程和時間成正比例的量。
點評:判斷兩種量是不是成正比例,分三步:一看它們是不是相關聯的兩種量;二是看一種量變化,另一種量是不是也隨著變化;滿足了前面兩個條件,再看它們的比值是否一定。不要省去任何一步。如果用字母x和y分別表示兩種相關聯的量,用k表示它們的比值,正比例關系可以用這樣的式子來表示:
例2、(判斷是否成正比例)
練習本的單價一定,買練習本的數量和總價是不是成正比例?為什么?
分析與解:根據正比例的意義,看兩個變量的比值是否一定,如果兩個變量的比值一定,那么這兩個變量就成正比例,反之,則不成正比例。
買練習本的數量和總價是兩種相關聯的量,它們與練習本的單價有下面的關系:

所以練習本的數量和總價成正比例。
例3、(正比例的圖像)磁懸浮列車勻速行駛時,路程與時間的關系如下。

(1)圖中的點A表示時間為1分鐘時,磁懸浮列車駛過的路程為7千米。請你試著描出其他各點。
(2)連接各點,它們在一條直線上嗎?
(3)根據圖像判斷,列車運行2分半鐘時,行駛的路程是多少千米?行駛30千米大約需要幾分鐘?

分析與解:根據提供的各組數據描出圖像的許多個點,再依次連成直線。路程和時間相對應的數的比值都是7,即速度一定,路程和時間成正比例,圖像是一條直線。對照圖像,可以根據時間的值估計出路程的值,也可以根據路程的值估計出時間的值,估計時允許有一定的出入。
(1)描點、連線如圖。

(2)在一條直線上,因為路程和時間成正比例,正比例的圖像是一條直線。
(3)根據圖像,列車運行2分半鐘時,行駛的路程是17.5千米;行駛30千米大約需要4.3分鐘。
例4、(辨析)圓的周長和直徑成正比例,圓的面積和半徑成正比例?
分析與解:圓的周長和直徑成正比例,而圓的面積和半徑卻不成正比例。
可列表判斷。
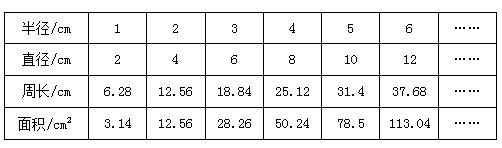
圓的周長和直徑的相對應的數的比值都是3.14,所以圓的周長和直徑成正比例。而圓的面積和半徑的相對應的數的比值是變化的,所以圓的面積和半徑不成正比例。
圓的周長和直徑成正比例,圓的面積和半徑卻不成正比例。
例5、(反比例的意義)
下表是王師傅加工一批零件時,每小時加工零件個數隨時間變化的情況。這兩種量有什么關系?

分析與解:
(1)從上表可以看出,表中有每小時加工零件的個數和加工的時間兩種量。
(2)從左往右看,每小時加工零件的個數擴大,加工的時間反而縮小;從右往左看,每小時加工零件的個數縮小,加工的時間反而擴大。所以它們是兩種相關聯的量。
(3)每小時加工零件的個數和相對應的加工的時間的積都始終不變,如20 × 12 = 240,30 × 8 = 240,40 × 6 = 240……而這個積就是這批零件的總個數。
通過觀察和計算,我們發現:每小時加工零件的個數和加工的時間是兩種相關聯的量,每小時加工零件的個數隨著加工的時間變化而變化,但無論它們怎么變化,相對應的積是一定的,有這樣的關系:每小時加工零件的個數 × 加工的時間 = 零件的總個數(一定)。
所以每小時加工零件的個數和加工的時間成反比例的量,它們之間的關系叫做反比例關系。
點評:判斷兩種量是不是成反比例,和正比例一樣,分三步:一看它們是不是相關聯的兩種量;二是看一種量變化,另一種量是不是也隨著變化;滿足了前面兩個條件,再看它們的乘積是否一定,進行判斷。不要省去任何一步。如果用字母x和y分別表示兩種相關聯的量,用k表示它們的比值,正比例關系可以用這樣的式子來表示:xy = K(一定)。

歡迎掃描二維碼
關注奧數網微信
ID:aoshu_2003

歡迎掃描二維碼
關注中考網微信
ID:zhongkao_com