1、如下圖,在一張由一組水平線和一組垂直線組成方格紙上,如果任意相鄰平行線之間的距離都相等,我們就把這樣兩組平行線的交點稱為格點(如下圖中的紅點),把圖中相鄰兩個格點的距離看著一個單位長度,把每個小正方形的面積看作一個面積單位(如圖中帶陰影的方格)。
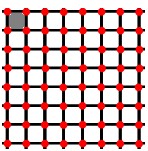
一個多邊形的頂點如果全是格點,這個多邊形就叫做格點多邊形,本講就,學習求格點多邊形的面積問題。這種格點多邊形的面積計算起來很方便,一般有三種方法:①規則的格點多邊形,可以運用多邊形的面積公式求出面積;②一些簡單而又特殊的格點多邊形,可以通過數格子求出面積;③較復雜的不規則圖形,一般用皮克公式計算。其中數格子的方法比較原始,很少用。
任意格點多邊形,只要數出多邊形周界上的格點的個數及圖內格點的個數,就可用下面的皮克公式算出面積:
格點多邊形面積=圖內格點個數+周界格點數÷2-1
這個公式是皮克(Pick)在1899年給出的,被稱為“皮克定理”,這是一個實用而有趣的定理。
皮克定理的證明:
將格點圖中的每個點看作以這個點為圓心、以單位面積正方形的邊長的一半為半徑的圓。格點多邊形圖內的點對應的圓的面積都是圖形面積的一部分;而在多邊形邊界上的點對應的圓的面積只有一半屬于這個多邊形,且多邊形每個角上的圓屬于圖內的面積都不到半個圓,少了其外角對應的扇形面積,因任意多邊形的外角和是360度,正好是個整圓,所以周界上圓在圖內的面積為:周界格點數÷2-1
所以格點多邊形面積為:圖內格點個數+周界格點數÷2-1。
皮克定理的證明過程比較抽象,孩子難以理解。本講只要求孩子初步認識格點面積公式,掌握格點面積公式的應用,到初中還會進一步學習皮克定理。
2、
【解析】:
圖①是個平行四邊形,周界上有10個格點,圖內有4個格點,根據格點面積公式,圖①的面積為:4+10÷2-1=8;
圖②是個梯形,周界上有8個格點,圖內有2個格點,根據格點面積公式,圖②的面積為:2+8÷2-1=5;
圖③是個三角形,周界上有6個格點,圖內有4個格點,根據格點面積公式,圖③的面積為:4+6÷2-1=6;
以上3個圖形都是規則圖形,但四年級學生還沒有學過這3種圖形的面積計算,不能用面積公式計算。
圖④是個六邊形,周界上有8個格點,圖內有9個格點,根據格點面積公式,圖④的面積為:9+8÷2-1=12。
這四個圖形也可以用數格子的方法計算面積。
3、
下圖中喇叭、小貓、小狗的面積各是多少?
【解析】:
這三個圖形都適合用格點面積公式計算面積。
喇叭周界上有8個格點,圖內沒有格點,面積為:0+8÷2-1=3;
小貓周界上有20個格點,圖內有2個格點,面積為:2+20÷2-1=11;
小狗圖案可以看著是兩個格點多邊形組成,先分別求出每個格點多邊形的面積,再求出總面積。
軀干面積:0+12÷2-1=5;
尾巴面積:0+4÷2-1=1;
總面積:5+1=6。
像小狗圖案這樣,由兩個或兩個以上獨立的格點多邊形拼成的多邊形,要求其總面積,一般先求出每個獨立多邊形的面積,再求和,以免發生漏數多個獨立圖形公共格點的錯誤。
下面是一個漂亮禮盒的平面圖,請你求出它的面積。
4、
【解析】:
這個禮盒平面圖是由3個獨立的格點多邊形組成的。
左邊三角形面積可以用皮克公式求出:4+4÷2-1=5;
右邊三角形面積可以用皮克公式求出:2+6÷2-1=4;
下面長方形長為6、寬為3,可以直接用長方形面積公式算出面積:6×3=18;
所以上圖總面積為:5+4+18=27。
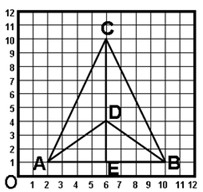
5、你知道下圖中共有多少個圖形嗎?每個圖形的面積各是多少?
【解析】:
這里所說的圖形既包括凸多邊形,也包括凹多邊形。圖中有8個三角形: AEC,AED,ADC,ABD,ABC,EBD,EBC,DBC;有3個四邊形:ADBC,ABDC,ABCD。
可以用皮克公式算出每個圖形的面積,例如四邊形ADBC的面積為:
21+8÷2-1=24。
其它圖形的面積:(略)。



